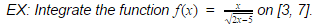THE FINAL BLOG POST

1. Finding antiderivatives is difficult because it is sometimes confusing to decide which methods to use, such as u-substitution, which is the most difficult concept for me. The hardest thing to do is a trigonometric function because it is difficult to memorize the derivatives/antiderivatives of those.

2. Find F(x) when f(x) = x^2-sin(x)     F(x)= (x^3)/3 + cos(x)

Find F(x) when (tan^2)x+3 dx

3. Find F(x) when f(x)= 3x^2 - 1/x^3    F(x)= x^3 - (x^-2)/2

1. Using U-Substitution to evaluate integrals is difficult because I always lose track of what to do with the du and what number to put out in front of the integral. I just make simple mistakes each time that cost me. I have only gotten a couple u-substitution questions right in my life. Out of numerous.

2.Find the definite integral of x(1 - 3x^2)^4dx

Find the definite integral of  (1+sec(x))^2(sec(x)tan(x))dx

Find f(x) when f(x) = x(2-3x)^1/2  dx

3.

1. I can find the area between two curves. This is difficult because the equations must be graphed to see which one is on top, but this concept as a whole is fairly easy, as a step into washer/disk method.

2. Find area of the region bounded by : f(x) = 2x-2    g(x) = -x^2-2x+3

Find area of the region bounded by : f(x) = 2x^3-1, g(x) = 2x-1

3.

 

1. Using Fundamental Theorem of Calculus Part I is not very difficult all, as long as I can remember what it is. And FTC Part 2 is a little harder but when I look in my binder and recall it I'm sure it won't be as difficult as I remember. Still don't know if  I did it right.

2.

3. 

1. Using disks is difficult when attempting to figure out what to subtract or add in the equation for me. I learned a trick, but the hard part will be recalling that. And remembering to take it in terms of x or y's.

2. Region bounded by f(x)= sqrt(x) and x=4 revolved about x axis.

3.

March Madness

1. The difference between rotating a horizontal line and vertical line:
A rotation over a horizontal line is taken in regards to x's, while a rotation over a vertical line is taken in regards to y's.

2. The difference between creating a washer and a disk is that a washer involves a gap in its rotation. This can be due to having 2 equations, or being bounded by more than one line.

3. Find the volume of the region bounded by y=x, x=3, and x=5, rotated about the x-axis.
Begin by creating a visual representation. Which I do not have.


Then, set up the equation. The interval is [3,5] because of the shaded region, and it is taken in regards to x because it is rotated about a horizontal line. The equation y=x is the radius.

3b. Find the volume of the region bounded by y= x^3, x=1, and x=2, and y=2, rotated about the y-axis.

The equation is on [1,8] because the equation must be taken in regard to y's, which are vertical. The area that won't be there, the middle of the washer, has a radius of 2, so it is subtracted from the 3D radius of  the cubed root of y and solved.

AND a throwback to the last time Illinois was decent enough to make the tournament.

POINTS

How to do it and what usually trips me up

I can use U-Substitution to integrate functions.

For U-substitution I have to take the piece of the equation that I want to use for u. In this case that will be 2x-5. (u= 2x-5) To find du I will have to take the derivative of u. (du= 2dx). To find the new interval I will plug 3 and 7 into the equation for u. The new interval will be: upper limit 9, lower limit 1. The equation will be f(x)= 1/2[integral 1 to 9](5/2u)/sqrt(u) dx. The part that usually trips me up is when I have to get rid of the x in the equation along with the dx. I often get confused on what cancels and what doesn't and end up with more pieces than necessary at the end of the problem. In this equation the only thing that cancels is the dx. So the equation will be: f(x)= 1/2[integral 1 to 9](5/2u)/sqrt(u).
  The next step is to find the antiderivative, so change the sqrt to a 1/2 power. f(x)=1/2[integral 1 to 9](5/2u)/(u^1/2). The antiderivative of this is f(x)= 2*(5/2u^2)/2/3(u^3/2). Plug your u value in and your integral values in: 2*(5/2(2x-5)^2)/2/3*((2x-5)^3/2). The final equation should involve x's, assuming I didn't do this wrong. Which I probably did and I'm going to check someone else's blog to see what the answer is.
 
I can find the area under the curve using the Fundamental Theorem of Calculus Part 2.

The fundamental theorem of calculus part 2 shows that the antiderivative of the upper limit minus the antiderivative of the lower limit equals the definite integral. In this case the antiderivative is F(x)= 2x^2 - 2x^3/ 3. 
Applying the upper limit: 2(12)^2 - 2(12)^3 /3. 288-576= -288
Applying the lower limit: 2(0)^2 - 2(0)^3 /3. 0-0=0
-288-0= -288 The part that usually gives me trouble in this concept is understanding the question. The area under the curve usually refers to rectangles and summation, so I have to look at the FTC part 2 to show me that it can be done a simpler way.

I can approximate the area under a curve via left and right endpoints for a given amount of rectangles.

What usually trips me up is keeping track of n's. Remembering which ones cancel at the end is difficult because even if some are left over, they're most likely going to equal 0.

To find the area under a curve you do summation. You take the number of rectangles over n and multiply by the summation. Then you insert the lower limit + i times the number of rectangles over n into the function. Then solve. The n's should cancel at the end and you will end up with a whole number.

Optimus Prime

1. Optimization is done by finding the derivative of a function, then setting it equal to zero. The final step is to solve for the variable. We use the derivative and the process of optimization to find the maximum or minimum. For example,

2. Find the point on the on the line y=2x+3 that is closest to the origin. To optimize, use the distance formula and the original equation. d= sqrt[(x-0)^2 + (y-0)^2]
Plug in the original equation for y in the distance formula. d= sqrt[x^2 + (2x+3)^2]
Remove the square root and take the derivative of the equation. (d^2)' = 2x + 2*(2x+3)*2
Solve for x. (d^2)'= 2x +8x+12
Set the equation equal to zero to solve. 0 = 10x + 12         -12 = 10x       x= -12/10    x= -6/5
Plug the x value back into y equals to find the point that is asked for in the original question and solve for y.  y = 2(-6/5)+3       y = -12/5 + 3     y = 3/5      
So the answer to the point that is closest to the origin is (-6/5, 3/5)


3. If f'(x) = 6x^2 -10x -1 then,

a)f(x) = 2x^3 -5x^2 -x + 7

b)f(x) = 2x^3 -5x^2 -x -15