How to do it and what usually trips me up
I can use U-Substitution to integrate functions.
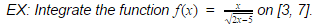
For U-substitution I have to take the piece of the equation that I want to use for u. In this case that will be 2x-5. (u= 2x-5) To find du I will have to take the derivative of u. (du= 2dx). To find the new interval I will plug 3 and 7 into the equation for u. The new interval will be: upper limit 9, lower limit 1. The equation will be f(x)= 1/2[integral 1 to 9](5/2u)/sqrt(u) dx. The part that usually trips me up is when I have to get rid of the x in the equation along with the dx. I often get confused on what cancels and what doesn't and end up with more pieces than necessary at the end of the problem. In this equation the only thing that cancels is the dx. So the equation will be: f(x)= 1/2[integral 1 to 9](5/2u)/sqrt(u).
The next step is to find the antiderivative, so change the sqrt to a 1/2 power. f(x)=1/2[integral 1 to 9](5/2u)/(u^1/2). The antiderivative of this is f(x)= 2*(5/2u^2)/2/3(u^3/2). Plug your u value in and your integral values in: 2*(5/2(2x-5)^2)/2/3*((2x-5)^3/2). The final equation should involve x's, assuming I didn't do this wrong. Which I probably did and I'm going to check someone else's blog to see what the answer is.
I can find the area under the curve using the Fundamental Theorem of Calculus Part 2.
The fundamental theorem of calculus part 2 shows that the antiderivative of the upper limit minus the antiderivative of the lower limit equals the definite integral. In this case the antiderivative is F(x)= 2x^2 - 2x^3/ 3.
Applying the upper limit: 2(12)^2 - 2(12)^3 /3. 288-576= -288
Applying the lower limit: 2(0)^2 - 2(0)^3 /3. 0-0=0
-288-0= -288 The part that usually gives me trouble in this concept is understanding the question. The area under the curve usually refers to rectangles and summation, so I have to look at the FTC part 2 to show me that it can be done a simpler way.
I can approximate the area under a curve via left and right endpoints for a given amount of rectangles.
What usually trips me up is keeping track of n's. Remembering which ones cancel at the end is difficult because even if some are left over, they're most likely going to equal 0.
To find the area under a curve you do summation. You take the number of rectangles over n and multiply by the summation. Then you insert the lower limit + i times the number of rectangles over n into the function. Then solve. The n's should cancel at the end and you will end up with a whole number.
