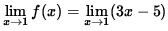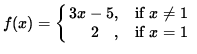1. Where continuity does not work
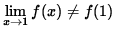The limit is approaching 1. When it is 1 it equals 2. When it's not 1, but very very close, it equals -2(plugged into the 3x-5 equation). So the limit is not continuous at 1 because the two equations do not match up.2. Intermediate Value Theorem
Use IVT to show a solution on [0,4] for f(x)= 2x^2 + 5x -3.
f(0)= 0 + 0 - 3= -3
f(4)= 32 + 20 - 3 = 49
Since f is continuous on [0,4] and f(0)= -3<0<49 =f(4), then there exists c (element) [0,4].
Use IVT to show a solution on [2,4] for f(x)= -2x^2 - 5x + 3.
f(2)= -8 - 10 + 3 = -15
f(4)= -32 - 20 + 3 = -49
Since f is continuous on [2,4] and f(2)= -49<0 but -49 is not less than 0 then it cannot be proved that there exists c (element) [2,4].
3. Types of Derivatives
Derivatives can be solved in two ways. The difference quotient
or the derivative in terms of slope.
Linear Derivative:
The derivative is -2.
The hardest part to finding a derivative is keeping track of the h's, or keeping track of what is being canceled.
4. Velocity
Instantaneous velocity is the slope of the tangent line at a certain point, but average velocity is the derivative that can be used to find the slope at any point.
