Monday, October 19, 2015

Calculus Continued...


$ \displaystyle{ \lim_{ x \to 1 } f(x) = \lim_{ x \to 1 } (3x-5) } $
$ f(x) = \cases{ 3x-5 ,& if $\space x \ne 1 $\space \cr \ \ \ \ 2 \ \ \ ,& if $ x = 1 $\space } $

1. Where continuity does not work

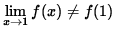$ \displaystyle{ \lim_{ x \to 1 } f(x) \ne f(1) } $The limit is approaching 1. When it is 1 it equals 2. When it's not 1, but very very close, it equals -2(plugged into the 3x-5 equation). So the limit is not continuous at 1 because the two equations do not match up.

2. Intermediate Value Theorem

Use IVT to show a solution on [0,4] for f(x)= 2x^2 + 5x -3.
f(0)= 0 + 0 - 3= -3
f(4)= 32 + 20 - 3 = 49
 Since f is continuous on [0,4] and f(0)= -3<0<49 =f(4), then there exists c (element) [0,4]. 

Use IVT to show a solution on [2,4] for f(x)= -2x^2 - 5x + 3.
f(2)= -8 - 10 + 3 = -15
f(4)= -32 - 20 + 3 = -49
 Since f is continuous on [2,4] and f(2)= -49<0 but -49 is not less than 0 then it cannot be proved that there exists c (element) [2,4].

3. Types of Derivatives

Derivatives can be solved in two ways. The difference quotient
or the derivative in terms of slope.
Linear Derivative:

The derivative is -2.
The hardest part to finding a derivative is keeping track of the h's, or keeping track of what is being canceled.

4. Velocity

Instantaneous velocity is the slope of the tangent line at a certain point, but average velocity is the derivative that can be used to find the slope at any point.
Posted by at

6 comments:

  1. rfmccuneOctober 19, 2015 at 12:39 PM

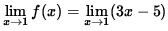
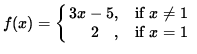
    Is agree that the most difficult part of finding the derivative is keeping track of what is being cancelled. (Scholarly Work)

    ReplyDelete
  2. ZachOctober 19, 2015 at 12:41 PM

    Your answer to number 4 is correct, but I would suggest adding an example to show that you know how to find instantaneous velocity and average velocity.

    ReplyDelete
  3. UnknownOctober 19, 2015 at 8:14 PM

    Looks like your answers are all here, most of them with examples to help the less scholarly out with their studies. I also agree with your answer about the difficulties of finding a derivative.

    ReplyDelete
  4. MattOctober 19, 2015 at 10:01 PM

    I find it very scholarly of you to provide examples that help explain the concepts you discuss. I also find it absurdly convenient that you went very in depth with the intermediate value theorem.

    ReplyDelete
  5. AnonymousOctober 25, 2015 at 12:17 PM

    You did not finish the statement on your first IVT. You said there is an element in the interval....... but gave a cliffhanger as to what that element does or will do.

    ReplyDelete
  6. UnknownNovember 5, 2015 at 10:19 AM

    Instead of saying "exists c (element)", you should say "exists an element c in"

    ReplyDelete

Subscribe to: Post Comments (Atom)